Reason in Revolt

Hyperbolic Geometry, Berkeley Math Circle

Posted at — Oct 31, 2024 by Izzy Meckler

These are my notes from a class at the Berkeley Math Circle on October 31rd, 2024. You can find an accompanying handout here.

Today we’re going to be talking about hyperbolic geometry.

But before we talk about that, first we have to talk about geometry. Ordinary geometry takes place on an infinite flat plane, like the whiteboard. We call this thing the Euclidean plane, after Euclid who was a Greek guy who developed geometry pretty extensively.

They invented geometry I guess so that they could do some construction or engineering but they ended up generalizing it way beyond that, into mathematics generally. They didn’t have a notion of numbers abstractly and even talked about numbers in terms of geometry.

The first relevant notions are distance and angle.

The next is a “straight line” which can be defined in terms of distance.

Challenge: how would you describe a straight line only using the notion of distance?

The first things we’re interested in with geometry are problems of measurement and arrangement. Measurement meaning: given a figure composed of lines, circles, etc., determine angles, lengths and areas of regions in the figure. Arrangement meaning: given constraints on areas, lengths and angles, does there exist a figure matching those constraints.

For example:

Problem (measurement): What is the sum of the angles in a pentagon? Does it depend on the pentagon?

Problem (arrangement): Draw a line $L$ and a point $p$ not on $L$. How many lines are there that pass through $p$ and are parallel to $L$?

Or, put another way, find all lines with distance 0 to $p$ and making a 0 degree angle with $L$.

An interesting property in Euclidean geometry is the possibility of scaling while preserving angles. If there is a figure with say total width $w$, there is another figure with total width $w'$ for any $w'$ in which all the angles and ratios between lengths stay the same.

This can be taken the defining property of Euclidean geometry which distinguishes it from other geometries. It can also be used to give an extremely simple proof of the Pythagorean theorem.

Problem: What happens to area when we scale? That is, if I have a figure $F$ with area $a$ and scale it by a factor $c$, what is the area of the scaled figure?

Problem: What is the sum of the angles in a triangle in the Euclidean plane? What does that actually mean geometrically?

Isometries in the Euclidean plane

Probably the best way to think about a geometry in general is to think about the transformations that preserve distances. You call such things isometries.

There are many transformations of the plane. Some preserve distances, some do not. If you are used to using image editing software where you can translate, reflect and rotate images, you are familiar with isometries.

One useful way of visualizing isometries is to imagine one plane sliding over another plane. Or in real life, imagine one piece of paper moving around on top of another one.

Question: what are some isometries?

What is useful about isometries? For one, they can allow you to put things in convenient positions for thinking about them. For example, some things may be easier to measure when you put them in a certain position.

Second, they are useful for proving the identity of angles and measurements.

For example consider the following:

Problem: You are given a triangle two of whose sides are equal (isoceles). Prove that two of the angles of the triangle are equal as well.

Let’s explore the isometries of the plane a bit. Three easy to understand kinds of isometries are reflections, rotations, and translations. Let’s try to show that this is all there is.

Convince yourself of the following by sliding around one piece of paper on top of another one:

Problem: Say $p$ gets mapped to itself by an isometry. What can this isometry be?

Problem: Pick a point $p$ in the plane and say it gets mapped to some point $q$ by an isometry. Where does the circle of radius 1 around $p$ get mapped to? Pick a point $p'$ on this circle and pick a point $q'$ for it to get mapped to. Is the behavior of the isometry on the rest of the plane fixed now?

Problem:Any isometry of the plane is determined by what it does to 3 points.

Problem: Prove that two distinct circles intersect in at most two points. Hint: prove the stronger statement that given 3 points there is exactly one circle containing all of them. Do you see why this implies what we want to prove?

Hyperbolic geometry

Now that we understand Euclidean geometry, we can begin to talk about hyperbolic geometry.

Hyperbolic geometry was only discovered relatively recently. In the 1820s/30s by Bolyai, Gauss, and Lobachevsky independently.

The hyperbolic plane is a 2 dimensional sort of space very similar to the Euclidean plane.

We can’t fit it exactly into Euclidean space without distortion, so I can only show you distorted pictures or models of parts of the Hyperbolic plane. We’ll start with a model called the upper half plane, or the Beltrami-Poincare plane. It consists of the $y > 0$ half of the xy plane.

We can tile the Euclidean plane with triangles

We can tile the hyperbolic plane by 45-30-90 triangles. Here is a picture of one such tiling.

All these triangles have the same size in the hyperbolic plane. They look different to us because we are Euclidean creatures. We should think

Here’s a tessellation of the hyperbolic plane based on a famous print by MC Escher. All these figures are the same size in the hyperbolic plane. They only appear to get smaller close to the boundary because of the distortion needed to make a Euclidean picture.

The true size of a figure at height $y$ is $1/y$ its apparent size. Or put another way, figures at height $y$ are drawn scaled by $y$. So figures at height $2$ are half as big as they appear to be (because they are drawn twice as big as they should), figures at height $1/2$ are twice as big as they appear to be etc.

In the hyperbolic plane one can speak of distances and angles, and therefore lines, circles, etc. The isometries even have some similarities. One can reflect through lines, rotate around points, and translate one point to another.

The first thing to know about hyperbolic geometry is, what are the “straight lines”. Remember that a straight line means the shortest path between points and not a Euclidean straight line. For example, the shortest path between here at the whiteboard and the back of this room involves going around the chairs, either to the left or right aisle, etc. and is far from a Euclidean straight line.

In the upper half plane model of the hyperbolic plane, the straight lines are

For example, the hyperbolic line between the point (0, 1) and the point (0, 2) is just the normal euclidean vertical line connecting these points.

How do we find the other hyperbolic lines, which recall are arcs of semi circles on the boundary. Here is how.

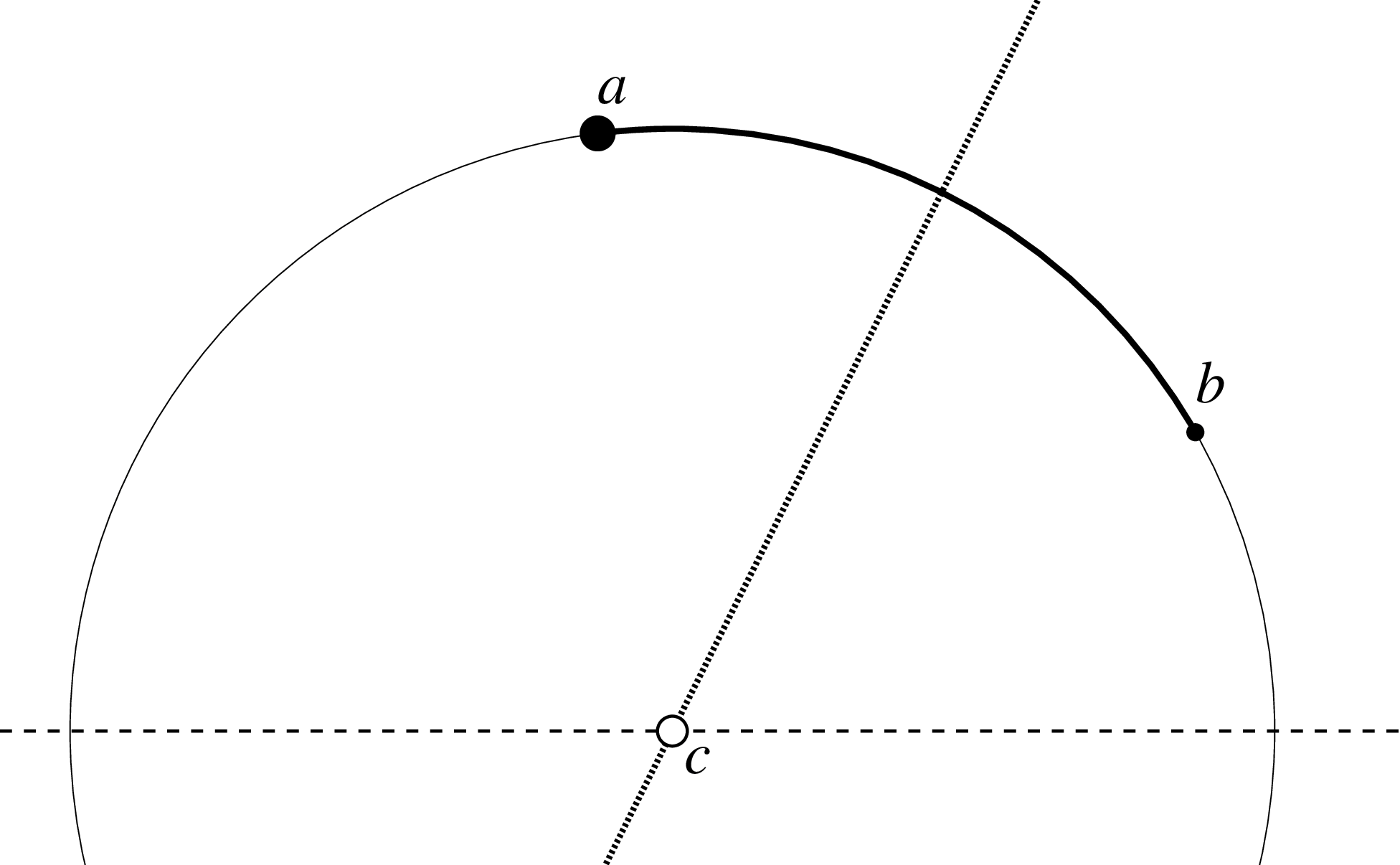
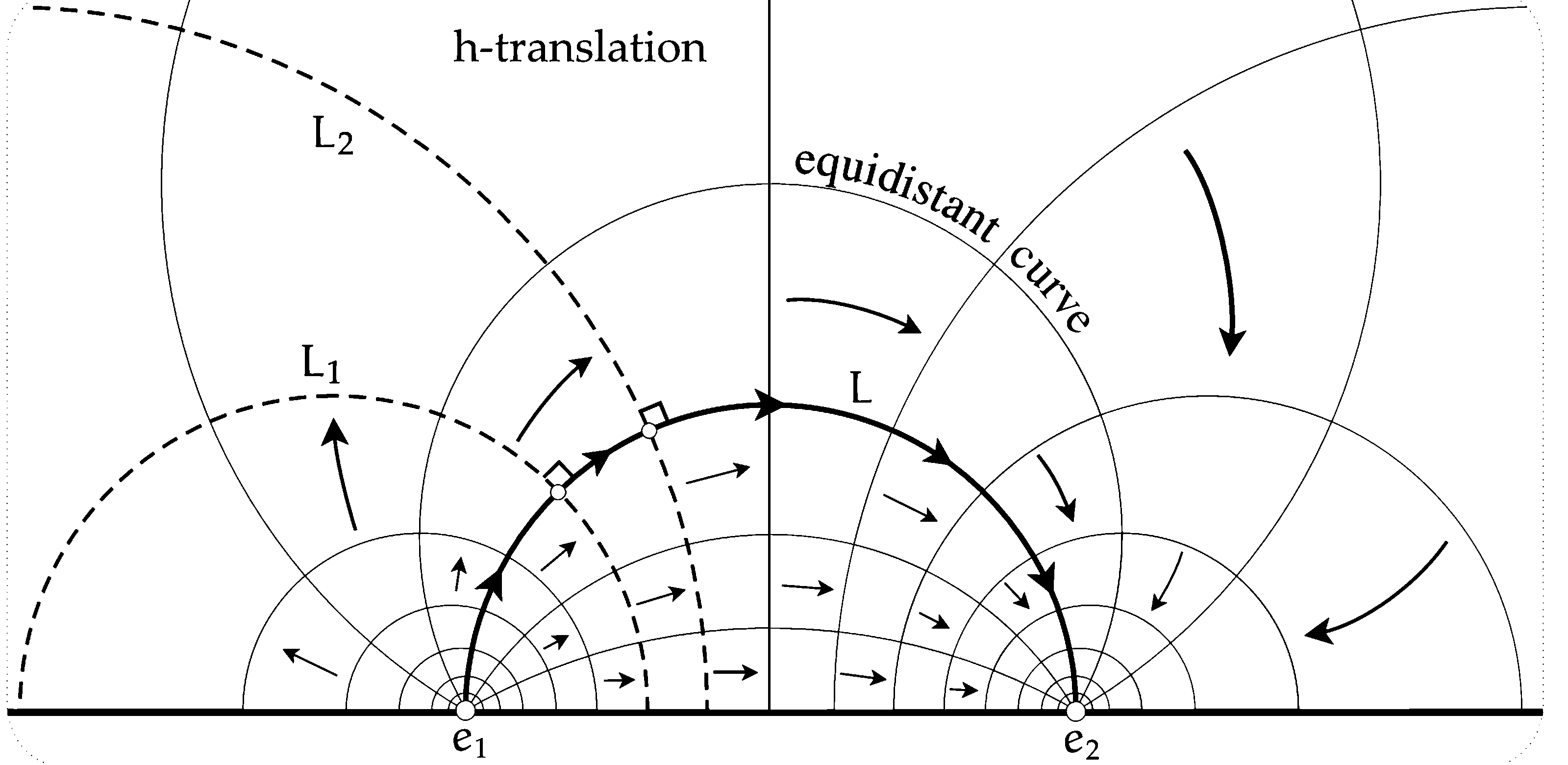
Say we are given points $a$ and $b$. We start by drawing the line equidistant from $a$ and $b$, the one that cuts space in half between them. This is illustrated as the line with the small dashes.

This hits the boundary (the x axis) at some point $c$. That point $c$ is the the center of the circle which serves as the straight line between $a$ and $b$. Remember that everything below the boundary (the horizontal dashed line) is not part of the hyperbolic plane and is only there to help us draw.

A “triangle” is 3 points connected by hyperbolic lines. Here’s a few triangles.

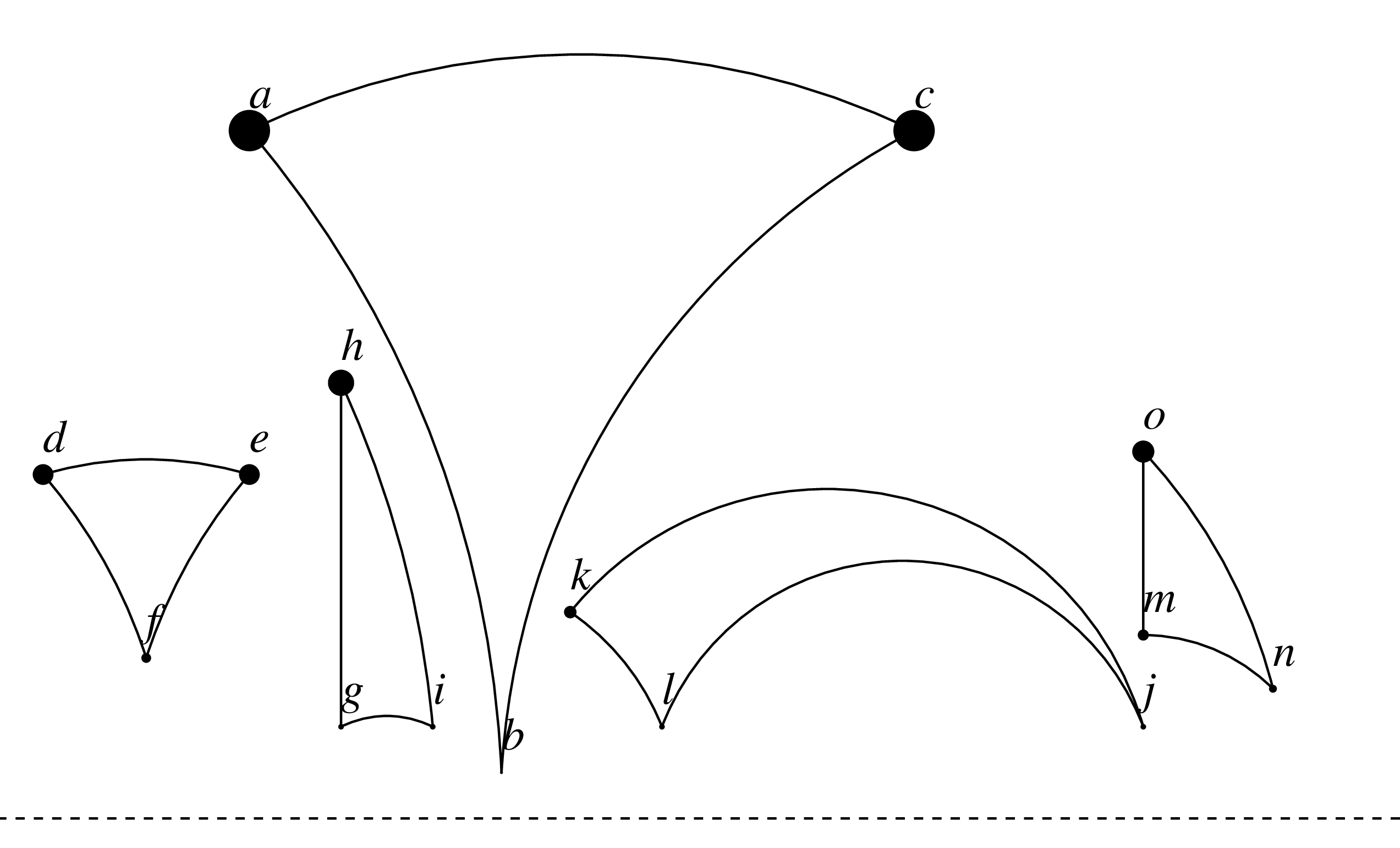
Angles are measured by measuring the angle between the tangents to the circles.

Question: what do you think the angles in each of these triangles add up to?

Here’s the same points with all the line segments extended to full lines so you get a sense of what lines look like.You can also see some hyperbolic quadrilaterals like the one containing $a$ and $c$.

Activity: draw hyperbolic lines between some points. You can find the center of the semicircle needed by following the steps in the above diagram: draw the line that cuts space in half between the two points, and find where it intersects the boundary line.

TODO pick up here . Have drawing of same triangle at different heights to illustrate how distance changes. Problem : are these two figures (triangles at same height differnt x) congruent? Why? Transition to isometry talk

Learning to work with the hyperbolic plane is a bit like learning to walk on a boat in the ocean. It will happen but it will take a little bit of time and trial and error.

Many properties are the same. Many however are different. Let’s start by investigating parallel lines.

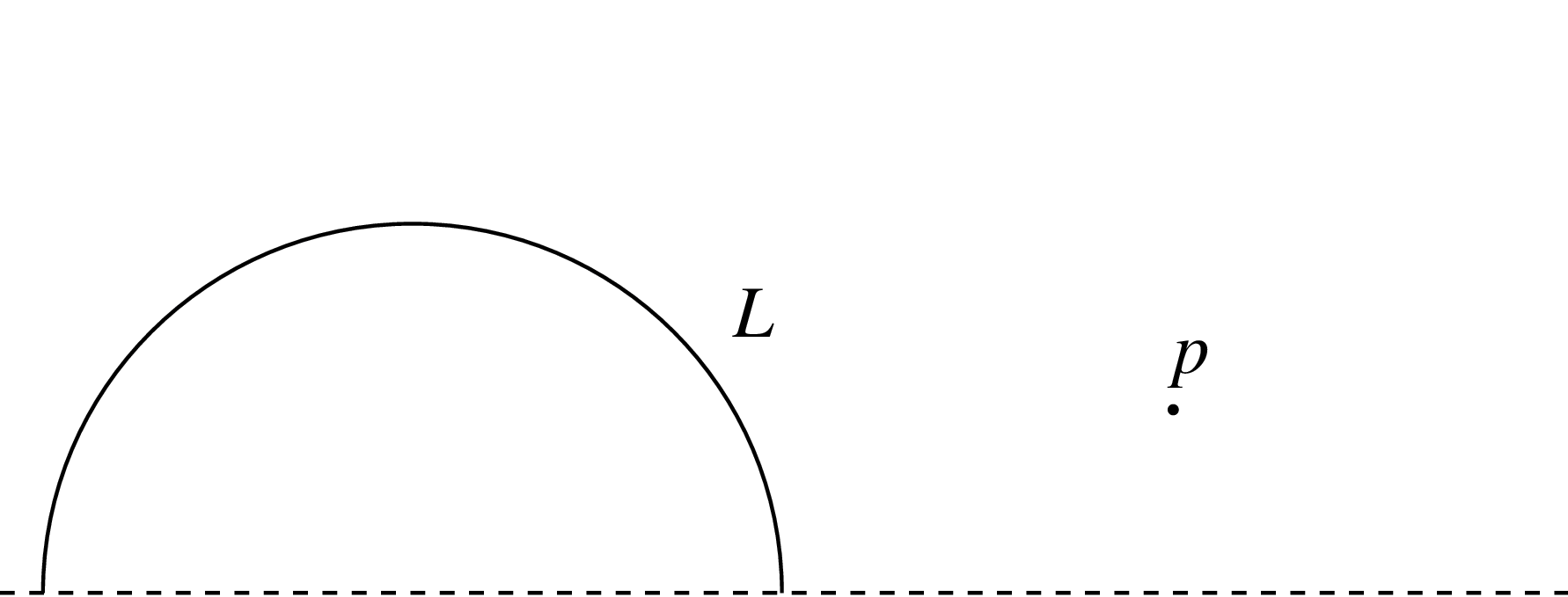
In Euclidean geometry, we saw that for any line $L$ and point $p$ there was exactly one line through $p$ parallel to $L$. Parallel here should be understood as meaning disjoint.

In hyperbolic geometry this is not the case.

Activity: given a hyperbolic line $L$ and a point $p$, find more than one line through $p$ that doesn’t intersect $L$.

Isometries

In the hyperbolic plane, these triangles have the same size 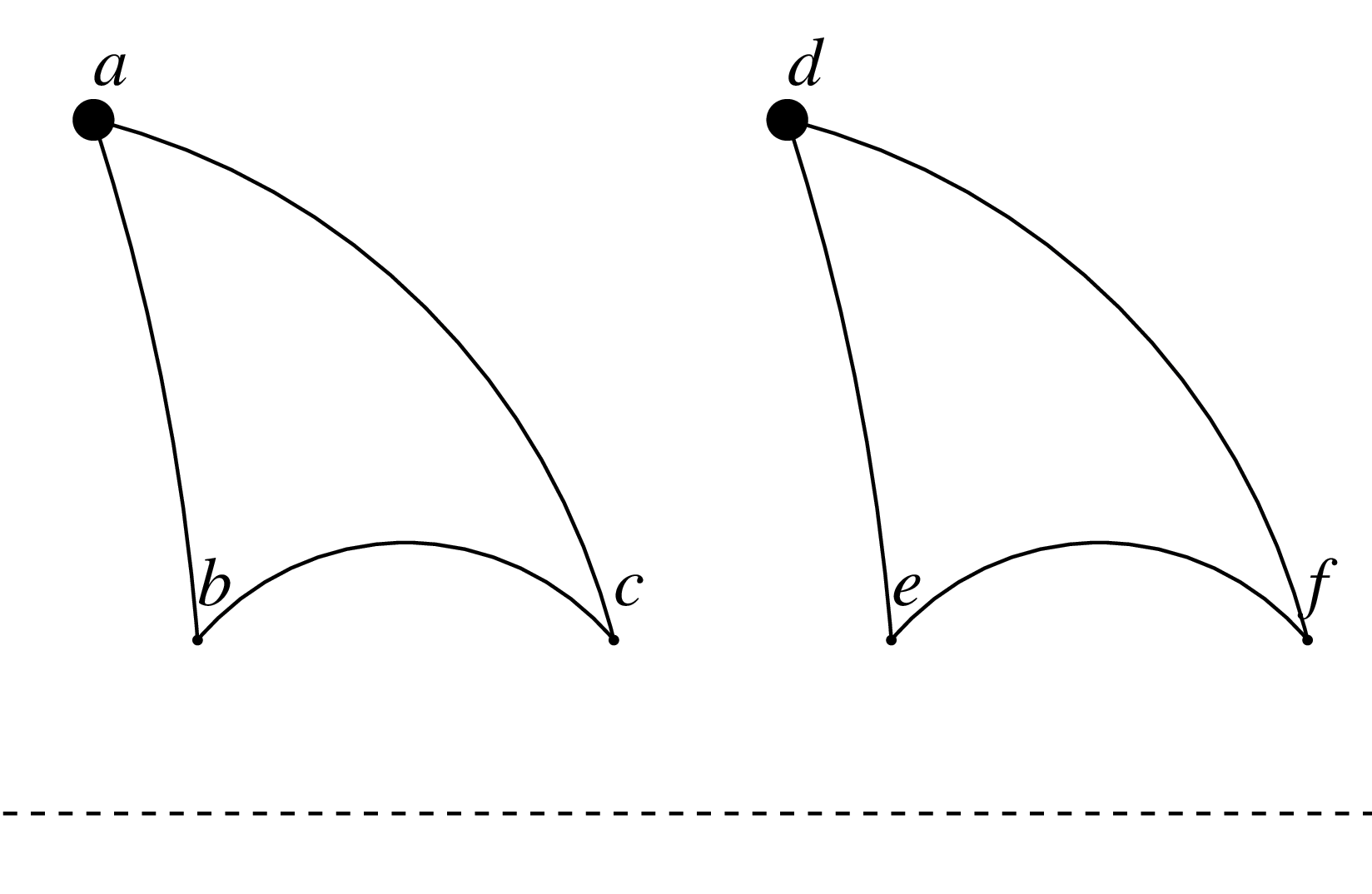There is an isometry taking one to the other. The isometry is just horizontal shifting (translation). This is an isometry because the distortion only depends on the height, so shifting left and right preserves size.

These two triangles also have the same size. Can you see why? The dashed lines give a clue.

Here is an illustration of the sort of isometry taking one of these triangles to the other. It is a dilation, a scaling of the whole plane centered at a point on the boundary.

Problem: explain why dilations being isometries is equivalent to saying that at height $y$ distances are $1/y$ times what they appear to be.

There are also rotations in the hyperbolic plane. Here is an illustration of a rotation around a point. 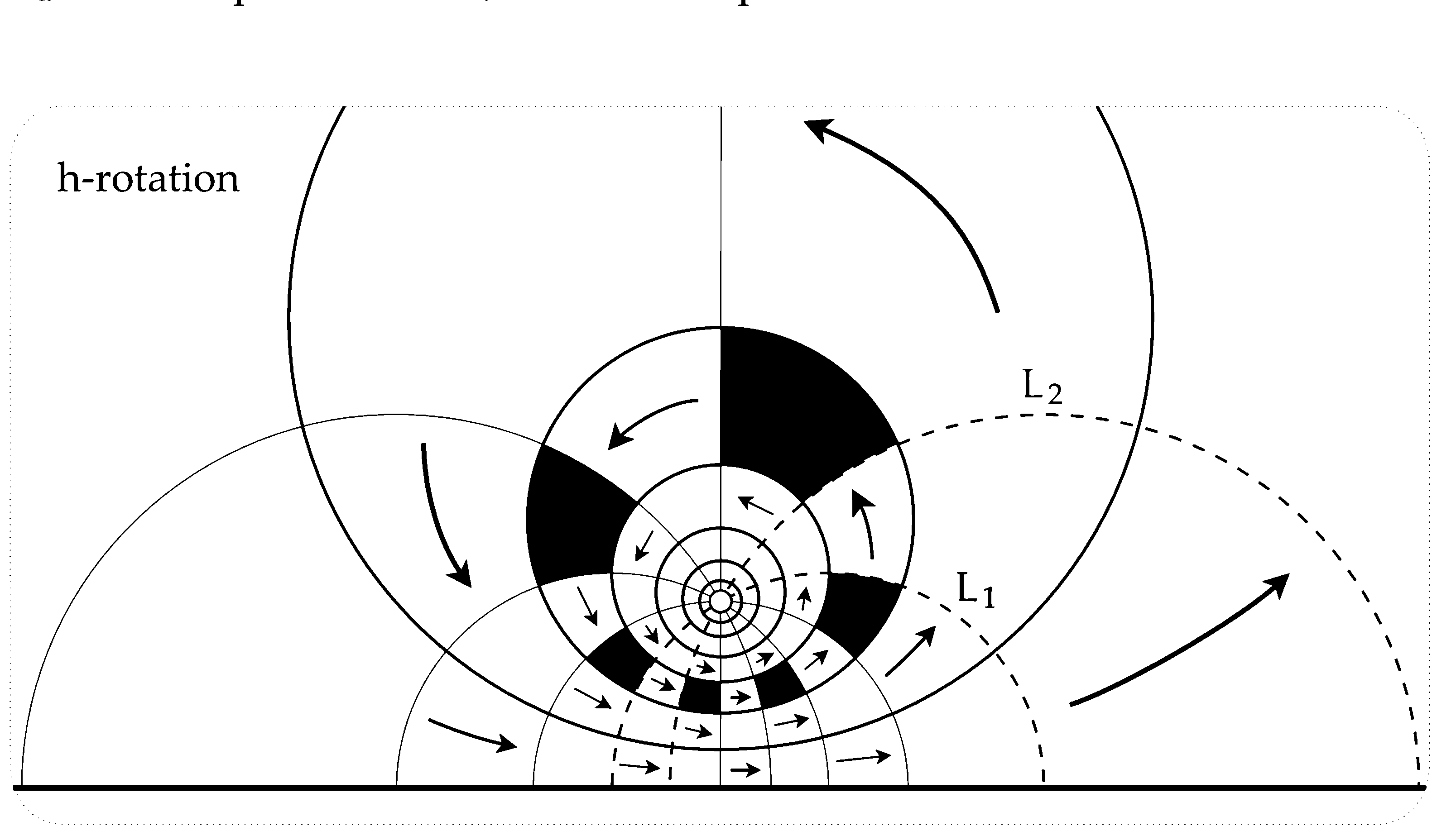We also have the analogue of translations And funky things called limit rotations, or parabolic isometries. 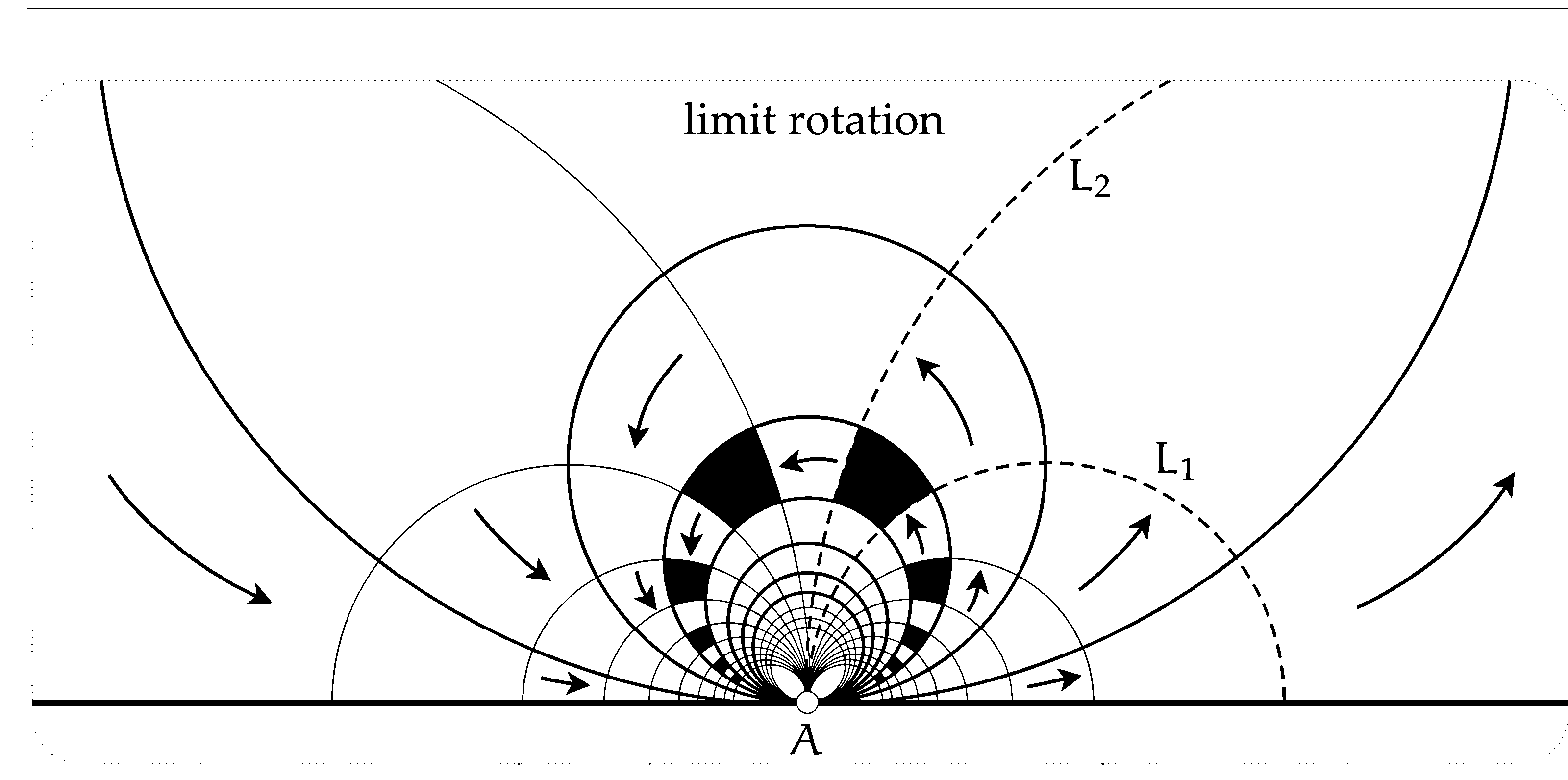Actually, we already saw one of these: the horizontal shifts are an instance. Can you see why?

Hyperbolic geometry, just like Euclidean geometry, has reflections too. Reflections work by circle inversion.

These isometries can be thought of in terms of the number of fixed points they have on the boundary. How many fixed points do these each have on the boundary?

If need more content, construct isometries by inversions by thinking about fixed points.

Problems

Activity: Draw some hyperbolic triangles and then use a dilation to draw one of the same size (even though it may look smaller or larger).

Problem: In the hyperbolic plane, you can make a triangle with any degree measurement as long as it adds up to less than 180. Prove this means you can make a hexagon with all angles equal to 90.

Challenge: given any 3 angles $a$, $b$, $c$, construct a triangle with the given angles.

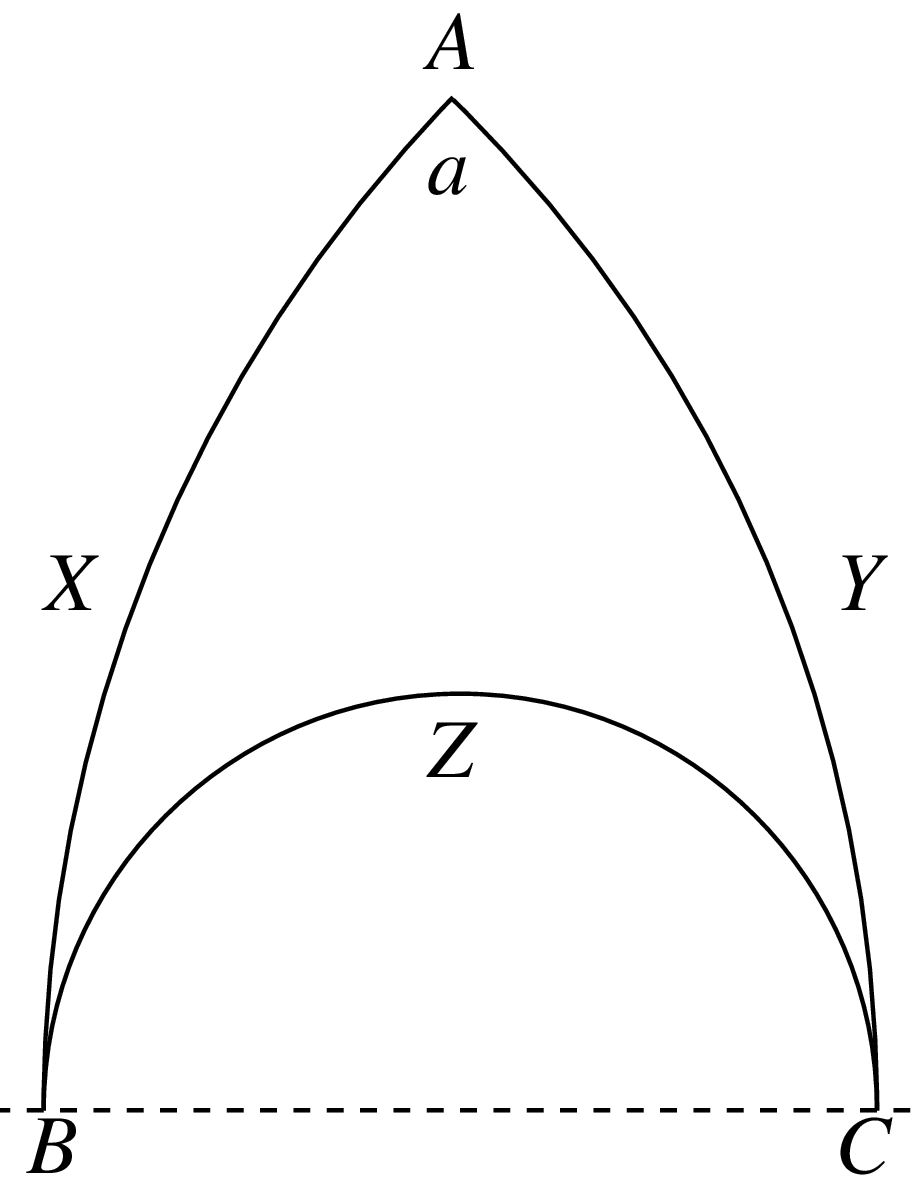
Here are some hints on how to do it. First, pick a point $A$ and draw lines $X$ and $Y$ coming out of $A$ with angle $a$ between them. These lines hit the boundary at points $B$ and $C$. Now draw the line going from $B$ to $C$.

Hint, use the following triangle as a starting point:

Recommend

https://geometrygames.org Jeff Weeks the shape of space

Activity: Tape together the paper triangles you have so that there are 7 triangles around every vertex.

Some observations about hyperbolic geometry for a Math Circle talk.

One needs a minimal theory of hyperbolic geometry for such a setting. There is no possibility of developing very explicit models using calculus: not enough time and the students do not have enough background. There is the possibility of giving descriptions of models in terms of their isometry groups. That may be a good way to go, especially in the case of the upper half plane where the isometries are extremely simple and can be understood without reference to calculus or complex numbers.

A good approach to finding out what to do would be: start with the theorems or ideas you’re interested in getting across and then figure out a minimal set of facts about hyperbolic geometry sufficient to prove those theorems or convey those ideas.

One fact of interest is the existence of limiting parallel lines: lines which do not intersect but which do come arbitrarily close to each other. How can we prove the existence of such lines.

Here is one proof:

In the upper half plan model, vertical Euclidean lines are hyperbolic lines. (This can be taken as axiomatic or proven using the fact that horizontal translations and dilations are isometries.) Take two (Euclideanly) parallel vertical lines. I claim their distance is going to zero as y goes to infinity. By the definition of distance between lines, it suffices to find pairs of points which have an arbitrarily short path connecting them.

Using translations and dilations put our two lines at $x=0$ and $x=1$ for convenience. Now, fix two points $(0, b)$ and $(1, b)$. We wish to estimate the length $L_b$ of the straight horizontal line path $\gamma_b$ between them. For example $L_1$ is the length of $\gamma_1$, the straight horizontal line path between $(0, 1)$ and $(1, 1)$.

Dilating by $b$ takes $(0, 1)$ to $(0, b)$ and $(1, 1)$ to $(b, b)$. It also takes $\gamma_1$ to the straight horizontal line connecting these points. That straight horizontal line (still of hyperbolic length $L_1$) can be decomposed into $b$ copies of $\gamma_b$ (connected by horizontal translation by $b$). Therefore $L_1 = b L_b$, or $L_b = L_1 / b$.

Thus, as $b$ goes to infinity, we get pairs of points which are closer and closer together. $\square$

This proof uses